多個城市源解析[1-3]結果顯示,PM10、PM2.5中,揚塵是主要的污染源,是大氣污染控制的重點。防風抑塵網利用空氣動力學原理,改變網后微環境[4],達到降低風速和減小揚塵的目的,是一種有效抑制開放性露天堆場散塵的措施,已在一些大型堆場得到了成功應用[5-7]。
國內外對防風抑塵網的研究取得了很有實用價值的成果。Lee等[8,9]模擬了抑塵網后二維料堆表面的壓力變化,得到孔隙率為40% ~50%時壓力衰減最大,并用粒子跟蹤測速技術顯示了網后三維料堆表面空氣速度、湍流強度和湍動能的衰減;Pack-wood[10]將防風抑塵網數值模擬結果與風洞試驗對比,得出了較好的一致性;DongZhibao等[11]將來流風分為滲流和繞流,并據速度梯度將網后劃分為7個特性區域,并研究了孔隙率對區域流場和區域數的影響;李建隆等[12]研究了抑塵網不同開孔形式對流場的影響,得出圓形開孔防風網的擋風效果最佳;劉建麟等[13],探究了組合風障對大尺度采礦區揚塵擴散的防風收塵效果。
目前對于防風抑塵網的研究,多單純集中于抑塵網孤立作用下網前網后空氣運動參數的變化特性等,至于料堆鈍體耦合網后湍流場導致網后空氣流場變化,尤其是對影響料堆起塵的表面風速廓線分布的影響鮮見報道。該研究通過CFD(computation-alfluiddynamics)數值模擬,對比不同孔隙率(0,0.2,0.3,0.4,0.6,1.0)下,料堆前后不同斷面處的風速廓線,17m(堆高),22m(網高),30m,40m,60m和80m高度壓力系數,分析料堆周圍的空氣動力結構,從而為抑塵網的優化設計提供數據支持。
1 數值模擬
1.1 物理模型
料堆是以一個典型三維棱臺為模型進行數值模擬。棱臺參數[14]設置為:下表面長154m,寬51m;棱臺高17m,上表面長113m,寬10m。抑塵網距料堆距離為1倍堆高,網長等于堆長。相關研究[15,16]表明,最佳網高在1~1.5倍的堆高范圍內,故網高取22m(1.3倍堆高)。計算區域的選擇對數值模擬的結果及精度至關重要,直接影響結果可靠性。計算區域過大會網格數多,增加不必要的計算時間;計算區域過小,邊界影響計算結果的準確性。針對計算域問題,課題組前期做了相關研究[17]得出,當計算區域長取14倍堆寬,寬度取2倍堆長,高度取7倍的堆高,堆前6倍堆寬時料堆表面剪切力這一宏觀量不再變化。所以計算區域取為714m×119m×308m的長方體。x方向沿堆寬方向,y方向沿堆高方向,z方向沿堆長方向,來流方向沿x正方向,如圖1所示。
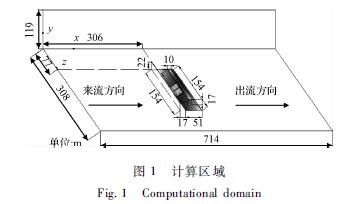
1.2 數學模型
物理模型選定后根據環境大氣湍流假設建立數學模型。料堆周圍的空氣流可視為不可壓縮恒定流,流動是穩態絕熱的。控制方程組包括質量守恒方程、動量守恒方程、湍動能方程和耗散率方程。如下所示。
質量守恒方程:

動量守恒方程:
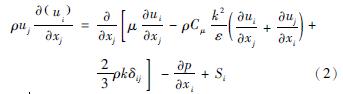
式中:Si為源項,該值在防風抑塵網區域內模擬為多孔介質的作用,源項由黏性損失項和慣性損失項兩部分組成:
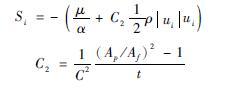
式中:α為多孔介質的滲透系數,m·s;C2 為慣性阻力因子,m-1;Ap 為板的總面積,m2;Af為孔的總面積,m2;t為抑塵網厚度,m,本文取0.002m;C近似等于0.98。
采用標準k-ε方程[18]來模擬三維流場,其中包括湍動能k方程和耗散率ε方程。
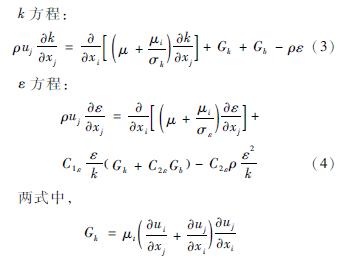
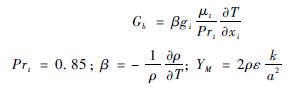
式中:ρ為空氣密度;ui、uj分別為i方向和j方向速度分量;xi、xj代表x、y方向的坐標;μ為空氣動力粘性系數;δij為克羅內克爾張量。具體參見http://www.jianfeilema.cn更多相關技術文檔。
對不可壓縮流體,Gb=0,YM =0,G3ε =0。
紊流系數C1ε、C2ε、C3ε、σε 和σk的取值較一致,分別為1.44、1.92、0.09、1.0和1.3。
詳情請下載:露天堆場防風抑塵網遮蔽效果的數值模擬


