景觀水體大多數都是靜止或者流動性較差的緩流水體，自凈能力差，易出現水體的污染和富營養化[1]。景觀水體的水質模擬與預測能為水質評價､水體富營養化與污染的控制以及水環境管理規劃等提供科學的依據[2]。

　　在水質模型中，存在著兩種學習型模型:人工神經網絡和支持向量機模型。然而，這兩種模型都存在著一定的局限性和缺點，如基于經驗風險最小化的人工神經網絡是一種在應用和試驗中建立的啟發式方法，可能出現局部最優[3]。而基于結構風險最優化的支持向量機方法在處理大規模的樣本時，往往需要求解復雜的二次規劃問題，計算復雜[4]。

　　組合預測是由Bates等[5]于1969年提出的一種預測方法，該方法在充分利用各個單一預測模型優點的基礎上，能克服單一模型的局限性和缺點，并最高效率地利用與挖掘數據信息，因而被廣泛地應用于水環境領域[6-9]。然而，實際情況往往是各單一模型是時間等一系列自變量的函數，在不同時刻模型變化也不相同，所以固定權重的分配方式自然無法體現這種關系。而變權重組合預測模型，提出權重隨時間等一系列自變量而變化的思想，避免固定權重的弊端[10]。所以，本文采用基于神經網絡與支持向量機2種模型，建立權重隨時間等一系列自變量而變化的變權組合模型，來應用于景觀水質的水質模擬與預測。

　　1 變權組合模型

　　1.1 神經網絡模型神經網絡(artificialneuralnetworks)是由大量的人工神經元廣泛地連接而成，用以模仿人腦神經網絡的復雜網絡系統。BP(back-propagation)神經網絡，即誤差反向傳遞的神經網絡，是將輸出誤差以某種形式通過隱含層向輸入層逐層反傳，并將誤差分攤給各層的所有單元，從而獲得各層單元的誤差信號，此誤差信號即作為修正各單元權值的依據。權值經過不斷的修正，最終得到可以滿足要求的BP神經網絡模型[11]。

　　1.2 支持向量機模型支持向量機(supportvectormachine)是一類新型的機器語言，它具有完備的統計學習理論和出色的學習性能，能根據有限的樣本信息在模型的復雜性和學習能力之間尋求最佳折衷，以求獲得最好的推廣能力[12]。對于非線性問題，支持向量機的基本思想是通過一個非線性映射將數據映射到高維特征空間，并在這個空間進行線性回歸[13]。

　　1.3 變權組合模型變權組合模型，其核心就是確定各個模型在各個時刻所占的權重，從而使模型更好地符合實際情況。對于m個單一預測模型得到的預測值f1，f2，…，fm，不妨假設每一個自變量對應一個相應的時刻，則其變權組合預測模型為:f(t) =Σmi=1gi(t)fi(t) (1)式中:t=1，2，…，n;i=1，2，…，m;fi(t)為第i個模型在t時刻的預測值;gi(t)為第i個模型在t時刻的權重，其滿足:1=Σmi=1gi(t) (2)假設gi(t)為t的連續函數，則gi(t)可以用p次多項式來表示:gi(t) =gi0·t0 +gi1·t1 +gi2·t2 +… +gip·tp(3)則:f(t) =Σmi=1gi(t)fi(t) =[f1(t)，f2(t)，…，fm(t)]g10 g11 … g1pg20 g21 … g2p… … … …gn0 gn1 … géêêêêëùúúúúûnpt0t1…téêêêêëùúúúúûn=Δ F(t)GT(t) (4)一旦gi(t)多項式的次數p確定，就可以通過廣義逆矩陣的循環迭代法[10]來求解系數矩陣G，并確定最終的變權組合預測模型。同時，從系數矩陣G的求解過程中可以發現，變權重組合預測方法其實就是根據m個單一預測模型在前n個時刻的預測值來確定某個時刻(某個自變量)的權重值，從而得到變權組合預測模型的預測值。

　　2 實例分析

　　2.1 基本資料本文選取天津市某園區的景觀水體作為研究對象，該景觀水體的水面面積約為29000m2，平均深度為3.6m，總容積約為10500m3，屬于典型的城市封閉緩流水體。水質監測點位于水體主體水域地帶，監測時間從2012年7月到2013年11月，共監測數據樣本為35個，監測指標包括水溫､pH值､氨氮､總氮､總磷和化學需氧量(COD)等水質指標。

　　COD作為一種表征水體有機物含量大小的重要指標，在一定程度上可以表示景觀水體的水質狀況和水體的污染情況。因此，本文建立COD與時間､水溫､pH值､氨氮､總氮和總磷之間變化關系的水質模型，通過COD的變化來了解當前景觀水體水質狀況，并為水質的預測預警作出科學的判斷與分析。

　　2.2 BP神經網絡模型本文利用該景觀水體從2012年7月到2013年11月的監測數據，建立BP神經網絡水質模型。由于各個水質監測指標值的量綱及數量級不同，在BP神經網絡訓練前要先對原始水質數據進行歸一化處理[14]，使得各個指標值落在[0，1]之間。對于歸一化方程，輸入時間t，是以2012年7月28號為第1天，以后各個監測時期的時間為實際監測日期與7月28號的時間距離，單位為天。然后再將輸入時間､水溫､pH值､氨氮､總氮､總磷和COD值采用歸一化公式(5)進行處理，公式如下:Xi = xi-xmin xmax -xmin(5)式中:xmin為原始監測值的最小值;xmax為原始監測值的最大值;xi為第i個原始監測值;Xi為歸一化處理之后的第i個監測值;

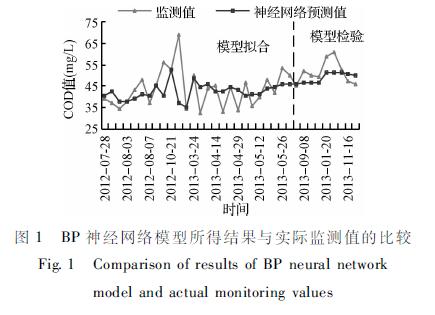
　　對于建立的BP神經網絡模型，輸入量包括時間､水溫､pH值､氨氮､總氮和總磷，輸出量為COD，隱含層的神經元采用Sigmoid型變換函數，輸出層則采用線性變換函數。而對于神經網絡結構中的各個參數確定則利用學習時間較短､精度與收斂性較好的L-__M算法，隱含層的節點數[15]則根據公式(6)確定:Ny =(Ns +Nj)0.5 +N (6)式中:Ny 為隱含層的節同時，將景觀水體水質監測樣本的數據分為訓練集､檢驗集兩個部分。用訓練集來訓練與擬合BP神經網絡，用檢驗集來對模型的預測結果進行檢驗。本模型中將前3/4的歸一化的數據作為BP神經網絡的訓練集，用后1/4的實際監測值作為BP神經網絡模型的檢驗集。利用MATLAB中的BP神經網絡工具箱，取訓練的最大循環次數epochs=10000，性能函數goal=0，最大驗證數據失敗的次數max_fail=20，最小的性能梯度值mingrad=0.00001。進行不斷地調試，發現在N=2，即隱含層的節點數Ny為4時，模型收斂性最好。模型結果與實際監測值的比較如圖1所示。具體參見http://www.jianfeilema.cn更多相關技術文檔。

詳情請下載：變權組合模型在景觀水體水質模擬中的應用