在活性污泥法污水生化處理過程的控制研究中，可以作為受控變量和操作變量的有許多，如何進行輸入輸出變量配對，已經有一些經驗法則，一般是與具體的工藝流程配置有關的。由于生化反應器內各子過程以及與二次沉降池之間的參數存在相互關聯，采用單回路控制時系統間必然存在耦合現象。因此在設計控制系統時，更多地應該把生化反應過程的主要受控變量和操作變量作為一個整體考慮，即構造多變量控制系統。

本文以體現系統內部硝化及反硝化生化反應進展狀況的2號生化反應器中的氨氮與硝酸氮濃度為被控對象，以溶解氧設定值(DO)及內循環流量為操作變量，采用活性污泥1號模型(AsM1)為控制器設計模型，設計了多變量預測控制算法。通過對ASM1模型的閉環控制仿真，結果表明多變量預測控制與傳統的帶解耦比例積分微分(PID)控制相比，在解耦和動態性能等方面具有更好的控制品質。

1 系統描述與控制方案設計

1．1 數學模型分析

典型的活性污泥法污水生化處理過程包括生化反應池和沉淀池，如圖1所示。其中反應池分為5個池，沉淀池分為1O層。其數學模型由于其內部復雜的機理關系而非常復雜，最常用的數學模型是國際水質協會1986年推出的ASM1模型n]，包含13種組分的變量，在流通中進行8個子反應過程。在每個生化反應池中，物料變化遵循物料平衡公式：

累積量 - 反應生成量 + 輸入量 - 輸出量(1)

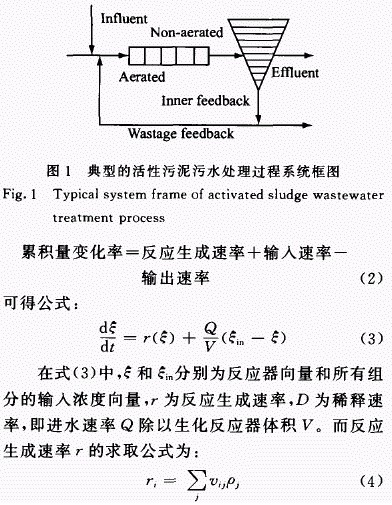
沉淀池的數學模型采用Takacs等。開發的二次指數沉淀速率模型模擬沉淀過程。由于在進行污水生化處理過程中的氮去除時，主要是控制生化反應中的硝化及反硝化反廊講程，缺氧區的末端即2號反應器內的S N0和S NH 最為關鍵，因此可將該號反應器內的S N0和S NH 作為被控變量。

1．2 控制系統結構分析

對ASM1模型來說，污水處理的水質控制指標一般是S N0和S NH 若采用單回路PID控制，當內循環流量Q和溶解氧濃度DO變化時S N0和S NH 都將隨之變化，兩路輸入與兩路輸出之間存在交叉耦合關系。

相對增益矩陣(RGA)[3]可用來分析多變量系統的變量間耦合關系，矩陣的各個元素反映了各輸出變量受輸入變量影響的程度。對ASM1模型在MATLAB／SIMULINK環境下進行仿真計算，得到內循環流量Q 和溶解氧濃度DO兩個操縱變量與被控變量氨氮濃度S NH 和硝酸氮濃度S N0的穩態增益矩陣為：

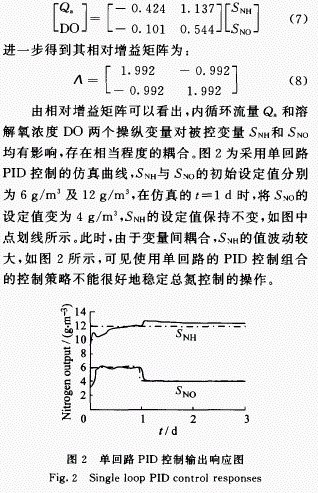
2 控制系統設計及仿真

由以上分析可知，如果分別對S NH 和 S N0  進行單回路控制，不能解決 nS NH 和 S N0  之間存在的耦合問題。如果其中的一個變量出現波動，必將影響到另外一個變量的值，使之也出現波動，因而擬對這兩個被控變量實施多變量預測控制方案。

首先采用穩態建模，在穩態下對Q 、DO施加階躍輸入，得到對象響應如圖3所示，從而獲得對象的預測模型。

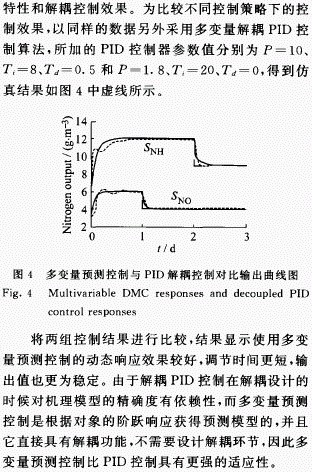
參考文獻：
[1] Henze M，Grady Jr C P L，Gujer W，et al，Activated sludge model No．1[A]．IAWPRC scientific and technical reports[c]．London：IAWPRC，1987．
[2] Takacs I，Party G G，Nolasco D．A dynamic model of the clari-fication thickening process[J]Water Research，1991，25(10)1263-1271．
[3] 王桂增．高等過程控制[M]．北京：清華大學出版社，2002．
[4] 舒迪前．預測控制系統及其應用[M]北京機械工業出版社，1996．作者: 鄭敏潔， 楊馬英